문제링크
https://www.acmicpc.net/problem/1707
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
문제설명
문제
그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.
출력
K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.
제한사항
- 2 ≤ K ≤ 5
- 1 ≤ V ≤ 20,000
- 1 ≤ E ≤ 200,000
| 제한시간 | 메모리제한 |
| 2초 | 256MB |
출처 : www.acmicpc.net
문제풀이
👨🏻💻 핵심 스킬 👨🏻💻
DFS
DFS를 사용하여 이분그래프를 구현할 수 있습니다. 정점을 두 집합으로 나누었을 때 집합 안의 정점끼리 간선이 구성되어있지 않으면 이분그래프라고 합니다. DFS 혹은 BFS를 사용하여 문제를 해결할 수 있습니다. 모든 정점을 확인할 때 DFS BFS모두 연결된 간선들로 체크를하게 됩니다. 그렇다면 집합으로 나누어 줄 때 연결된 간선끼리는 다른 집합으로 묶어주어야 함을 알 수 있습니다.
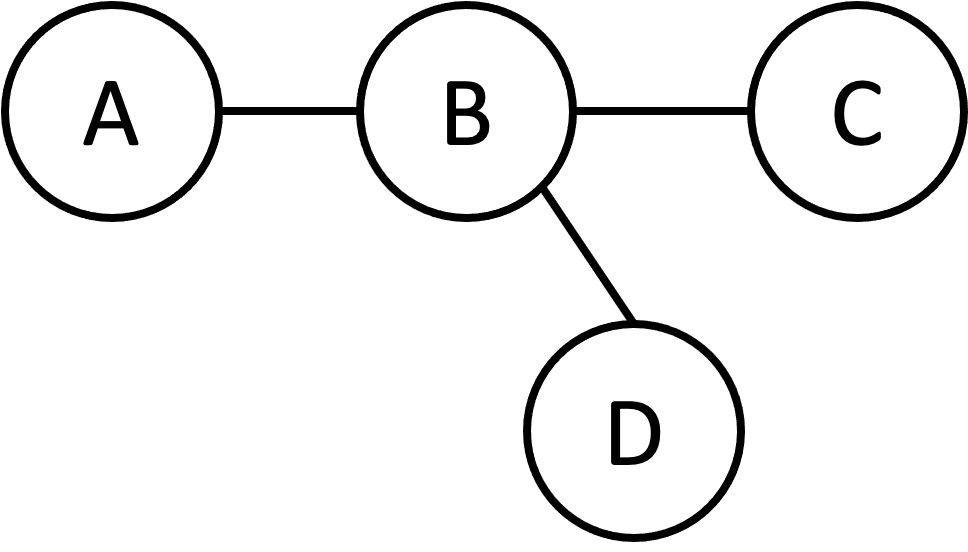
왼쪽과 같이 그래프가 구성되어 있다고 가정하여 설명드리겠습니다. A에서부터 DFS로 탐색을 하여주면 A 이후 B가 선택됩니다. 이 때 A와 B는 간선으로 구성되어 있으므로 같은 집합으로 묶을 경우 이분그래프의 조건을 만족하지 못합니다. 따라서 A와 B를 다른 집합으로 체크하여야 합니다. 그리고 다음으로 B에서 C를 체크합니다. 그렇게 될 경우 C는 B와 연결되어 있으므로 C와 B는 다른 집합으로 구분해주어야 합니다. 다음 D를 확인할 때도 B에서 불러준 것이므로 B와는 다른 집합으로 구분해야합니다.
따라서 최종적으로 이 그래프는 $(A,C,D)$와 $(B)$로 집합을 이루면 이분그래프를 만족하는 그래프라고 할 수 있습니다.
DFS나 BFS를 사용해 탐색할 때 간선을 통해 탐색을 하기 때문에 자신을 탐색하기 위해 불러준 노드와 다른 집합으로 구분을 지으면 이분그래프인지 확인이 가능하다는 것을 알았습니다. 이번에는 이분그래프가 아닐 경우를 알아보려고 합니다. 이분그래프가 아닌지 확인하는 경우는 각 정점에 대해 확인할 때 알 수 있습니다. 만약, 이미 과거에 체크된 정점이라면 어느 정점에 의해 이미 집합이 구분이 되어있는 정점일 것입니다. 자신과 연결된 정점중 체크가 된 정점이 자신과 같은 집합으로 속해 있다면 이는 이분그래프가 될 수 없습니다. 이를 확인하여 이분그래프인지 아닌지 최종적으로 알 수 있습니다.
그리고 이분 그래프의 연결요소가 한개가 아닐 수 있습니다! 여러개일 경우 모든 연결요소를 확인하여 이분그래프를 만족하는지 체크해주어야합니다.
구현코드
package backjoon_1707;
import java.util.ArrayList;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int testSize = sc.nextInt();
for (int i = 0; i < testSize; i++) {
int vertexCount = sc.nextInt();
int edgeCount = sc.nextInt();
boolean[] checked = new boolean[vertexCount + 1];
boolean[] position = new boolean[vertexCount + 1];
ArrayList<Integer>[] adLists = new ArrayList[vertexCount + 1];
makeRelationEdge(sc, vertexCount, edgeCount, adLists);
boolean result = true;
for(int j = 1; j <= vertexCount && result; j++){
if(!checked[j]){
result = dfs(j, adLists, checked, position);
}
}
if (result)
System.out.println("YES");
else
System.out.println("NO");
}
}
private static boolean dfs(int x, ArrayList<Integer>[] adLists, boolean[] checked, boolean[] position) {
checked[x] = true;
ArrayList<Integer> adList = adLists[x];
for (int i = 0; i < adList.size(); i++) {
int vertex = adList.get(i);
if (!checked[vertex]) {
if (position[x])
position[vertex] = false;
else
position[vertex] = true;
if (!dfs(vertex, adLists, checked,position))
return false;
} else {
if(position[vertex] == position[x])
return false;
}
}
return true;
}
private static void makeRelationEdge(Scanner sc, int vertexCount, int edgeCount, ArrayList<Integer>[] adList) {
for (int i = 1; i <= vertexCount; i++) {
adList[i] = new ArrayList<>();
}
for (int i = 0; i < edgeCount; i++) {
int first = sc.nextInt();
int second = sc.nextInt();
adList[first].add(second);
adList[second].add(first);
}
}
}
시간복잡도
$O(V+E)$
'CodingTest > Backjoon' 카테고리의 다른 글
| [BOJ_7576] 토마토 (java) (0) | 2021.12.16 |
|---|---|
| [BOJ_2667] 단지번호붙이기 (java) (0) | 2021.12.16 |
| [BOJ_11724] 연결요소 (java) (0) | 2021.12.14 |
| [BOJ_2156] 포도주 시식 (java) (0) | 2021.11.28 |
| [backjoon_11057] 오르막 수 (Java) (0) | 2021.11.21 |
![[BOJ_1707] 이분그래프 (java)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FeafRDU%2FbtruITqLyzw%2F88PFU9tWtWsFLWl1eXZ30k%2Fimg.png)